Question

Use Gaussian elimination on the augmented matrix, then use back substitution to find the solution of the system of linear equations.

-2x + 3y - 4z = 7

5x - y + 2z = 13

3x + 2y - z = 17

Answer 1

x = 4

y = 1

z= -3

Explanation:

Given equations are

-2x + 3y - 4z = 7

5x - y + 2z = 13

3x + 2y - z = 17

We can write the above equations in matrix augmented form as

`\left[\begin{array}{ccc}-2&3&-4:7\\5&-1&2:13\\3&2&-1:17\end{array}\right]`

`R_1=>(R_1)/(-2)`

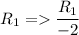
`=\ \left[\begin{array}{ccc}1&(-3)/(2)&2:(-7)/(2)\\5&-1&2:13\\3&2&-1:17\end{array}\right]`

`R_2=>R_2-5R_1\ and\ R_3=>\ R_3-3R_1`

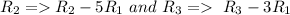
`=\ \left[\begin{array}{ccc}1&(-3)/(2)&2:(-7)/(2)\\0&-1+(15)/(2)&-8:13+(35)/(2)\\0&0&-7:17+(21)/(2)\end{array}\right]`

`=\ \left[\begin{array}{ccc}1&(-3)/(2)&2:(-7)/(2)\\\\0&(13)/(2)&-8:(61)/(2)\\\\0&(13)/(2)&-7:(55)/(2)+(21)/(2)\end{array}\right]`

`R_2=>\ (2)/(13)R_2`

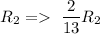
`=\ \left[\begin{array}{ccc}1&(-3)/(2)&2:(-7)/(2)\\\\0&1&(-16)/(13):(61)/(13)\\\\0&(13)/(2)&-7:(55)/(2)\end{array}\right]`

`R_3=>R_3-(13)/(2)R_2`

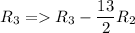
`=\ \left[\begin{array}{ccc}1&(-3)/(2)&2:(-7)/(2)\\\\0&1&(-16)/(13):(61)/(13)\\\\0&0&1:-3\end{array}\right]`

So, from the above augmented matrix, we can write

`x+(-3)/(2)y+2z=(-7)/(2).......(1)`

`y+(-16)/(13)z=(61)/(13)......(2)`

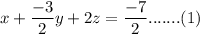
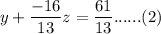
z= -3.....(3)

From eq(2) and (3)

`y+(-16)/(13)(-3)=(61)/(13)`

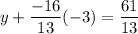
=> y = 1

Now, by putting the value of y and z in equation (1), we will get

`x+(-3)/(2)(1)+2(-3)=(-7)/(2)`

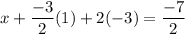
=> x = 4

Hence, the value of

x = 4

y = 1

z= -3