Question

A normal curve with mean = 25 has an area of .3531 between 25 and 34. What is the standard deviation for this normal curve?

Answer 1

The desviation is 8 4/7 or 8.571

Explanation:

The conversion for any variable X to a standard z is

`Z=\frac{X-\[Mu]}\\{\[Sigma]}`

where mu is the mean and sigma de desviation

You can find the value of Z whith the tables of the accumulated probability function. The accumulated probability for the mean is 0.5 .Remenber that the accumlated probability function represent the area at the left of an abscissa. Then

0.5+0.3531=0.8531

Acording to the accumulated probability function table, a Z=1.05 has an area of 0.8531 at its left.

Now it is only solving the equation

`\[Sigma]=(X-\[Mu])/(Z)`

σ=
`(34-25)/(1.05)`

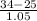
σ=8.571