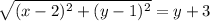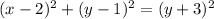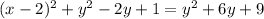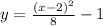Question

Using a directrixof y = -3 and a focus of (2, 1), what quadratic funtion is created

Answer 1

The function is a parabola described by:
`y = 1 +((x-2)^(2))/(8)`

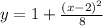
Explanation:

Since a directrix and a focus are given, then we know that they are talking about a parabola.

We know that the distance from any point in a parabola (x, y), to the focus is exactly the same as the distance to the directrix. Therefore, in order to find the required equation, first we will compute the distance from an arbitrary point on the parabola (x, y) to the focus (2, 1):

`d_(pf) = √((x-2)^2+(y-1)^2)`

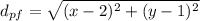
Next, we will find the distance from an arbitrary point on the parabola (x, y) to the directrix (y= -3). Since we have an horizontal directrix, the distance is easily calculated as:

`d_(pd)=y-(-3)=y+3`

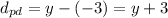
Finally, we equate the distances in order to find the parabola equation:

`√((x-2)^2+(y-1)^2)=y+3`

`(x-2)^2+(y-1)^2=(y+3)^2`

`(x-2)^(2) +y^(2)-2y+1=y^(2)+6y+9`

`(x-2)^(2)-8=8y`

`y = ((x-2)^(2))/(8)-1`