Evaluate 1^3 + 2^3 +3^3 +.......+ n^3

Question

asked Jan 13, 2020 232k views

1 Answer

Marthin · Answer 1 · 2020-01-18T12:21:30+0000

Notice that

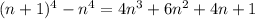
(n+1)^4-n^4=4n^3+6n^2+4n+1

so that

$\displaystyle\sum_(i=1)^n((n+1)^4-n^4)=\sum_(i=1)^n(4i^3+6i^2+4i+1)$

We have

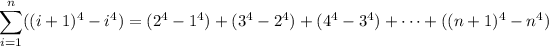
$\displaystyle\sum_(i=1)^n((i+1)^4-i^4)=(2^4-1^4)+(3^4-2^4)+(4^4-3^4)+\cdots+((n+1)^4-n^4)$

$\implies\displaystyle\sum_(i=1)^n((i+1)^4-i^4)=(n+1)^4-1$

so that

$\displaystyle(n+1)^4-1=\sum_(i=1)^n(4i^3+6i^2+4i+1)$

You might already know that

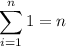
$\displaystyle\sum_(i=1)^n1=n$

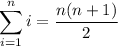
$\displaystyle\sum_(i=1)^ni=\frac{n(n+1)}2$

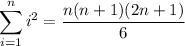
$\displaystyle\sum_(i=1)^ni^2=\frac{n(n+1)(2n+1)}6$

so from these formulas we get

$\displaystyle(n+1)^4-1=4\sum_(i=1)^ni^3+n(n+1)(2n+1)+2n(n+1)+n$

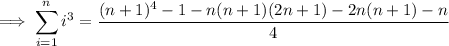
$\implies\displaystyle\sum_(i=1)^ni^3=\frac{(n+1)^4-1-n(n+1)(2n+1)-2n(n+1)-n}4$

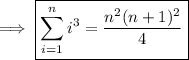
$\implies\boxed{\displaystyle\sum_(i=1)^ni^3=\frac{n^2(n+1)^2}4}$

If you don't know the formulas mentioned above:

The first one should be obvious; if you add
copies of 1 together, you end up with
.
The second one is easily derived: If
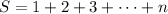$S=1+2+3+\cdots+n$ , then
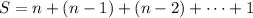$S=n+(n-1)+(n-2)+\cdots+1$ , so that
or
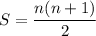$S=\frac{n(n+1)}2$ .
The third can be derived using a similar strategy to the one used here. Consider the expression
, and so on.