Question

Find the distance between a point (– 2, 3 – 4) and its image on the plane x+y+z=3 measured across a line (x + 2)/3 = (2y + 3)/4 = (3z + 4)/5

Answer 1

Distance of the point from its image = 8.56 units

Explanation:

Given,

Co-ordinates of point is (-2, 3,-4)

Let's say

`x_1\ =\ -2`

`y_1\ =\ 3`

`z_1\ =\ -4`

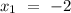
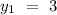
Distance is measure across the line

`(x+2)/(3)\ =\ (2y+3)/(4)\ =\ (3z+4)/(5)`

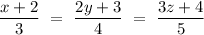
So, we can write

`(x-x_1+2)/(3)\ =\ (2(y-y_1)+3)/(4)\ =\ (3(z-z_1)+4)/(5)\ =\ k`

`=>\ (x-(-2)+2)/(3)\ =\ (2(y-3)+3)/(4)\ =\ (3(z-(-4))+4)/(5)\ =\ k`

`=>\ (x+4)/(3)\ =\ (2y-3)/(4)\ =\ (3z+16)/(5)\ =\ k`

`=>\ x\ =\ 3k-4,\ y\ =\ (4k+3)/(2),\ z\ =\ (5k-16)/(3)`

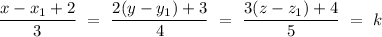
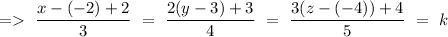
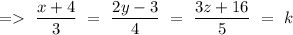
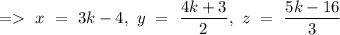
Since, the equation of plane is given by

x+y+z=3

The point which intersect the point will satisfy the equation of plane.

So, we can write

`3k-4+(4k+3)/(2)+(5k-16)/(3)\ =\ 3`

`=>6(3k-4)+3(4k+3)+2(5k-16)\ =\ 18`

`=>18k-24+12k+9+10k-32\ =\ 18`

`=>\ k\ =(13)/(8)`

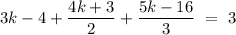
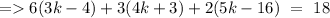
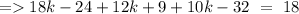
So,

`x\ =\ 3k-4`

`=\ 3* (13)/(8)-4`

`=\ (7)/(4)`

`y\ =\ (4k+3)/(2)`

`=\ (4* (13)/(8)+3)/(2)`

`=\ (19)/(4)`

`z\ =\ (5k-16)/(3)`

`=\ (5* (13)/(8)-16)/(3)`

`=\ (-21)/(8)`

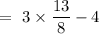
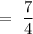
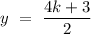
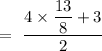
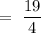
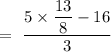
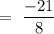
Now, the distance of point from the plane is given by,

`d\ =\ √((x-x_1)^2+(y-y_1)^2+(z-z_1)^2)`

`=\ \sqrt{(-2-(7)/(4))^2+(3-(19)/(4))^2+(-4+(21)/(8))^2}`

`=\ \sqrt{((-15)/(4))^2+((-7)/(4))^2+((9)/(8))^2}`

`=\ \sqrt{(225)/(16)+(49)/(16)+(81)/(64)}`

`=\ \sqrt{(1177)/(64)}`

`=\ 4.28`

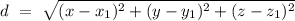
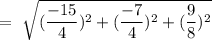
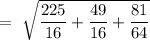
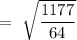
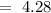
So, the distance of the point from its image can be given by,

D = 2d = 2 x 4.28

= 8.56 unit

So, the distance of a point from it's image is 8.56 units.