Question

A line segment has (x1, y1) as one endpoint and (xm, ym) as its midpoint. Find the other endpoint (x2, y2) of the line segment in terms of x1, y1, xm, and ym. Use the result to find the coordinates of the endpoint of a line segment when the coordinates of the other endpoint and midpoint are, respectively, (1, −9), (2, −1) and (−2, 18), (5, 9).

Answer 1

Answer:(3,7) for the first line, and (12,0) for the second one.

Explanation:

Hi Isabella,

1) The Midpoint of a line, when it comes to Analytical Geometry, is calculated as Mean of two points it follows:

Explanation:

Answer 2

(3,7) for the first line, and (12,0) for the second one.

Explanation:

Hi Isabella,

1) The Midpoint of a line, when it comes to Analytical Geometry, is calculated as Mean of two points it follows:

`x_(m)=\frac{x_(1) +x_(2) } {2}, y_(m) =(y_(1)+ y_(2) )/(2)`

2) Each segment has two endpoints, and their midpoints, namely:

a) (1,-9) and its midpoint (2,-1)

b) (-2,18) and its midpoint (5,9)

3) Calculating. You need to be careful to not sum the wrong coordinates.

So be attentive!

The first line a

`2=(1+x_(2) )/(2)\\  4=1+x_(2)\\  4-1=-1+1+x_(2) \\ x_(2)=3\\-1=(y_(2)-9)/(2)\\-2=y_(2)-9\\+2-2=y_(2)-9+2\\ y_(2)=-7`

So (3,7) is the other endpoint whose segment starts at (1,-9)

The second line b endpoint at (-2,18) and its midpoint (5,9)

`5=(-2+x_(2) )/(2) \\ 10=-2+x_(2) \\ +2+10=+2-2+x_(2)\\ x_(2)=12 \\ \\ 9=(18+y_(2) )/(2) \\ 18=18+y_(2) \\ -18+18=-18+18+y_(2)\\ y_(2) =0`

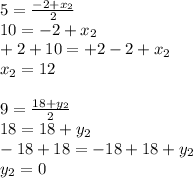
So (12,0) it is the other endpoint.

Take a look at the graph below: