Question

Pulsed lasers used in science and medicine produce very short bursts of electromagnetic energy. If the laser light wavelength is 1062 nm (this corresponds to a Neodymium-YAG laser), and the pulse lasts for 34 picoseconds, how many wavelengths are found within the laser pulse?

How short would the pulse need to be to fit only one wavelength?

Answer 1

Step-by-step explanation:

Given that,

Wavelength of the laser light,
`\lambda=1062\ nm=1062* 10^(-9)\ m`

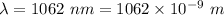
The laser pulse lasts for,
`t=34\ ps=34* 10^(-12)\ s`

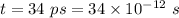
(a) Let d is the distance covered by laser in the given by,
`d=c* t`

`d=3* 10^8* 34* 10^(-12)`

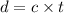
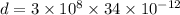
d = 0.0102 meters

Let n is the number of wavelengths found within the laser pulse. So,

`n=(d)/(\lambda)`

`n=(0.0102)/(1062* 10^(-9))`

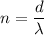
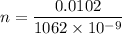
n = 9604.51

(b) Let t is the time need to be fit only in one wavelength. So,

`t=(\lambda)/(c)`

`t=(1062* 10^(-9))/(3* 10^8)`

`t=3.54* 10^(-15)\ s`

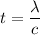
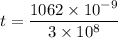
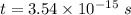
Hence, this is the required solution.