Question

The finishing time for cyclists in a race are normally distributed with an unknown population mean and standard deviation. If a random sample of 25 cyclists is taken to estimate the mean finishing time, what t-score should be used to find a 98% confidence interval estimate for the population mean?

Answer 1

2.485

Explanation:

Answer 2

The T-score is 2.49216

Explanation:

A 98% confidence interval should be estimated for the end times of cyclists. Since the sample is small, a T-student distribution should be used, in such an estimate. The confidence interval is given by the expression:

`[\bar x -T_{(n-1,(\alpha)/(2))} (S)/(√(n)), \bar x +T_{(n-1,(\alpha)/(2))} (S)/(√(n))]`

`n = 25\\\alpha = 0.02\\T_{(n-1;(\alpha)/(2))}= T_((24;0.01)) = 2.49216`

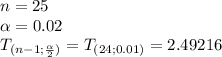
Then the T-score is 2.49216