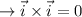Question

Given any triangle in the plane, associate to each side an outward pointing normal vector of the same length as the side. Show that the sum of these three vectors is always 0.

Answer 1

Let , a, b and c be the length of three sides of triangle, represented in terms of vectors as
`\vec{a},\vec{b},\vec{c}`.

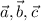Now, vector of same Magnitude acts as normal vector to each side.

So, equation of any vector p having normal q is given by

`\vec{p} *\vec{q}`

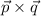
Now sum of three vector and it's normal is given as

`=\vec{a} *\vec{a}+\vec{b} *\vec{b}+\vec{c} *\vec{c}\\\\=0+0+0\\\\=0`

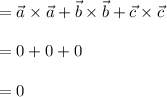
Cross product of two identical vectors is Zero.

`\rightarrow \vec{i} *\vec{i}=0`