Question

A hydrogen atom, initially at rest, absorbs an ultraviolet photon with a wavelength of λ=121.3nm. Part A: What is the atom's final speed if it now emits an identical photon in a direction that is perpendicular to the direction of motion of the original photon?

Part B: What is the atom's final speed if it now emits an identical photon in a direction that is opposite to the direction of motion of the original photon?

Answer 1

Step-by-step explanation:

Momentum of a photon

= h / λ

Where h is plank's constant and λ is wave length of photon

h = 6.6 x 10⁻³⁴ Js and λ = 121.3 x 10⁻⁹ m

momentum of photon

=
`(6.6*10^(-34))/(121.3*10^(-9))`

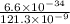
= 5.44 x 10 ⁻²⁷ Ns

Momentum of hydrogen atom

= 5.44 x 10 ⁻²⁷ Ns

When hydrogen atom emits another photon in perpendicular direction , according to Newton's second law , it acquires additional momentum of equal magnitude in opposite direction to the direction of emission of photon. Hence it has two similar momentum in perpendicular direction.

The resultant momentum

=
`√(2)` x 5.44 x 10⁻²⁷

= 7.7 x 10⁻²⁷ Ns

B ) When hydrogen atom emits another photon in opposite direction , according to Newton's second law , it acquires additional momentum of equal magnitude in opposite direction to the direction of emission of photon. Hence it has two similar momentum in acting in the same direction.

The resultant momentum

= 2 x 5.44 x 10⁻²⁷ Js.

= 10.88 x 10⁻²⁷ Js