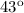Answer:
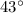
Step-by-step explanation:
According to Snell’s Law:
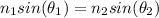
Where:
 is the first medium index of refraction (glass)
is the first medium index of refraction (glass)
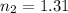 is the second medium index of refraction (ice)
is the second medium index of refraction (ice)
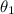 is the angle of the incident ray
is the angle of the incident ray
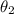 is the angle of the refracted ray
is the angle of the refracted ray
In this context, the index of refraction is a number that describes how fast light propagates through a medium or material.
Now, the critical angle
 is the angle from which there is no refraction and all the incident light is reflected to the same medium from which it proceeds, that is, the total internal reflection occurs. This is only possible when the index of refraction of the medium where the light strikes is higher than the index of refraction of the other medium, then the second angle (the exit angle) will reach the
is the angle from which there is no refraction and all the incident light is reflected to the same medium from which it proceeds, that is, the total internal reflection occurs. This is only possible when the index of refraction of the medium where the light strikes is higher than the index of refraction of the other medium, then the second angle (the exit angle) will reach the
 , for this critical incident angle
, for this critical incident angle
 .
.
Since
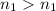 ,
,
![\theta_(1)=[tex]\theta_(c)](https://img.qammunity.org/2020/formulas/physics/college/lr0k9av2w2k0v2kpx3a2mzx8elgtdn5d8z.png) [/tex] and
[/tex] and
 , hence:
, hence:
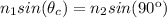
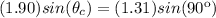
Isolating
 :
:

Finally:
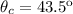
The option that is close to this value is