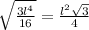Question

Use Heron's formula for triangular area to derive the area of an equilateral triangle with side length x.

THIS IS FOR MATH 4312. HISTORY OF MATH

Answer 1

A=
`(l^(2)√(3))/(4)`

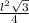
Explanation:

Firstly, let's take the Heron's formula, which allows us to calculate the area of any triangle without the need of knowing the value of the height or the angle. Just the half of perimeter, and each side of a triangle.

A =
`√(p(p-a)(p-b)(p-c))`

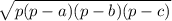
p = Semi perimeter (Half of Perimeter)

2p =Perimeter (sum of all the values)

Keep in mind, that in an equilateral angle all of the sides have the same value, so to make things easy let's call, a, b and c just by one variable l

2) Replacing it in Heron's Formula:

`√(p(p-l)(p-l)(p-l))`

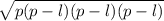
The semiperimeter of an Equilateral Triangle is

P =
`(l+l+l)/(2)` =
`(3l)/(2)`

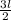
3) Inserting all of that in the Heron's Formula

`\sqrt{(3l)/(2)((3l)/(2) -l)((3l)/(2) -l)((3l)/(2) -l)`

`\sqrt{(3l)/(2)*((l^3)/(8))}`

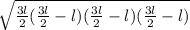
Finally we can derive the Equilateral Triangle Area through Heron's:

`\sqrt{(3l^4)/(16) } =(l^(2)√(3))/(4)`