Question

One urn contains 8 blue balls and 12 white balls, and a second urn contains 14 blue balls and 5 white balls. An urn is selected at random, and a ball is chosen from the urn. (Round your answers to one decimal place.) (a) What is the probability (as a %) that the chosen ball is blue? (b) If the chosen ball is blue, what is the probability (as a %) that it came from the first urn? Need Help? Read It Talk to a Tutor

Answer 1

a) The probability that the chosen ball is blue is 56.84%

b) If the chosen ball is blue, there is a 35.19 probability that it came from the first urn.

Explanation:

a) What is the probability (as a %) that the chosen ball is blue?

First the urn is chosen, then the ball. There can be a blue ball from urn 1 and from urn 2.

-The probability of a blue ball being chosen from urn 1 is:

40%(8 blue balls among 20 in urn 1, 8 of 20 is 40%) of 50%(the chance of urn 1 being chosen is 50%)

So
`P_(1) = 0.4*0.5 = 0.20`

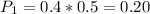
-The probability of a blue ball being chosen from urn 2 is:

73.68%(14 blue balls among 20 in urn 2, 14 of 19 is 73.68%) of 50%(the chance of urn 2 being chosen is 50%)

So
`P_(2) = 0.7368*0.5 = 0.3684`

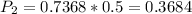
The probability that the chosen ball is blue is
`P = P_(1) + P_(2) = 0.20 + 0.3684 = 0.5684 = 56.84`%.

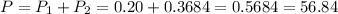b) If the chosen ball is blue, what is the probability (as a %) that it came from the first urn?

This item can be formulated as the following problem:

What is the probability of B happening, knowing that A has happened.

It can be calculated by the following formula

`P(B/A) = (P(B).P(A/B))/(P(A))`

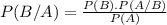
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.

In this item, A(what has happened) is the ball being blue. In item a), we found that P(A) = 0.5684.

B is the blue ball coming from the first urn. P(B), the probability of the first urn being chosen, is 50% = 0.5.

P(A/B), the probability of the blue ball being chosen from the first urn is 40% = 0.4.

So:

`P(B/A) = (0.5*0.4)/(0.5684) = 0.3519 = 35.19%`

If the chosen ball is blue, there is a 35.19 probability that it came from the first urn.