Question

The mass of a newborn baby’s brain has been found to increase by about 1.6 mg per minute. (a) How much does the brain’s mass increase in one day? (b) How much time does it take for the brain’s mass to increase by 0.0075 kg?

Answer 1

a) The mass of the baby's brain increases 2304mg in one day.

b) It takes 4687.5 minutes for the brain’s mass to increase by 0.0075 kg

Explanation:

This can be solved by a simple rule of three.

In a rule of three problem, the first step is identifying the measures and how they are related, if their relationship is direct of inverse.

When the relationship between the measures is direct, as the value of one measure increases, the value of the other measure is going to increase too. Otherwise, when the relationship between the measures is inverse, as the value of one measure increases, the value of the other measure will decrease.

In this problem, the measures are the time and the baby's mass. As time increases, so will the baby's mass. It means that we have a direct rule of three.

Question a:

The problem states that the newborn brain's mass increases 1.6mg a minute. A day has 24 hours of 60 minutes, so a day has 24*60 = 1440 minutes.

So, we have the following rule of three:

1 minute - 1.6mg

1440 minutes - xmg

x = 1440*1.6 = 2304mg

The mass of the baby's brain increases 2304mg in one day.

Question b:

A kilogram has
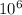`10^6`mg. So 0.0075kg = 75000 mg. The brain's mass increases 1.6mg per minute. How many time it takes to increase by 75000mg.

1 minute - 1.6mg

x minutes - 7500mg

`x = /frac{7500}{1.6}`

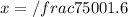
It takes 4687.5 minutes for the brain’s mass to increase by 0.0075 kg