Question

27 test scores in a math class have a standard deviation of 12.3. Use a .05 significance level and to test that this class has a standard deviation less than 14.1. State the null and alternative hypotheses, the p-value, and conclusion.

Answer 1

Answer: The standard deviation of test scores in the class is not less than 14.1

Explanation:

Let's suppose that the test scores follow a normal distribution. Besides, we have:

a) Standard deviation
`s=12.3`

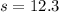
b) Significance level
`\alpha =.05`

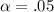
c) n=27

Using a) we can deduce that sample variance
`s^(2) = s*s = 151.29`.

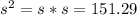Since we want to prove if the population variance is less than
`14.1^(2)`:

`H_(0)` (Null hypotesis) :
`\sigma^(2) =(14.1)^(2)`

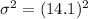
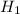`H_(1)` (Alternative hypotesis):
`\sigma^(2) \leq (14.1)^(2)`

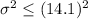
For test this kind of hypotesis (variance in one population) the correct test statistic is
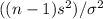`((n-1)s^(2))/\sigma^(2)`, which under
`H_(0)` have Chi-square distribution with n-1 degrees of freedom.

Calculating the test statistic (
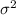`\sigma^(2)` is the value in
`H_(0)` ) :

`((27-1)*(151.29))/((14.1)^2) = 19.79`

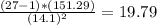
For this hypotesis (left one tailed test) the p-value is
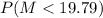`P(M<19.79)` where M follow a Chi-square distribution with n-1=26 degrees of freedom.You can check in a chi-square table that p-value=0.1986

If
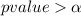`pvalue>\alpha` then there is no evidence to statistically reject
`H_(0)` . Therefore, the standard deviation of test scores in the class is not less than 14.1 (95% confidence level).