Question

Find the unit vectors that are parallel to the tangent line to the parabola y = x2 at the point (2, 4).

Answer 1

The unit vectors are:

`\vec u_1 = \left<\cfrac1{√(17)}, \cfrac4{√(17)}  \right>\\\vec u_2 = \left<-\cfrac1{√(17)}, -\cfrac4{√(17)}  \right>`

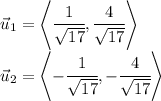
Explanation:

Unit vectors that are a parallel to the tangent line have the same slope than the tangent line, thus we can find the slope of the tangent line, find directional vectors and then their corresponding unit vectors.

Finding the slope of the tangent line.

We can find the first derivative of the curve, which represents the slope of the tangent line of the curve at that point.

`y = x^2 \\ y'=2x`

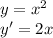
At x = 2 we have

`y'= 2(2)\\y'= 4\\`

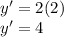
Thus we have slope m = 4, then the parallel unit vector has slope m = 4/1

Finding unit vectors.

From the slope m = 4/1, we can write it as a direction vector with x =1 and y = 4. Notice also that x = -1 and y = -4 would have given as as well slope m = 4 too.

`\vec u =<1, 4>`

Then in order to find the unit vector on that direction we can use the formula

`\hat u =\cfrac{\vec u}\vec u`

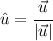
So finding the magnitude we get

`|\vec u |= √((1)^2+(4)^2)\\|\vec u| = √(17)`

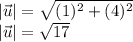
Then one unit vector that is parallel to the tangent line is

`\vec u_1 = \left<\cfrac1{√(17)}, \cfrac4{√(17)}  \right>`

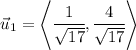
And the second unit vector is

`\vec u_2 = \left<-\cfrac1{√(17)}, -\cfrac4{√(17)}  \right>`

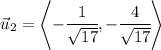
The negative sign on both x and y components just tell us that we are aiming on the opposite direction as the first unit vector, yet both have the same value of the slope.