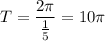Answer:
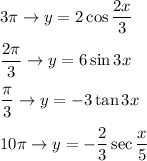
Explanation:
The period of the functions
 ,
,
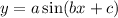 ,
,
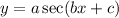 or
or
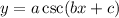 can be calculated as
can be calculated as
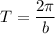
The period of the functions
 or
or
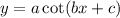 can be calculated as
can be calculated as
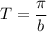
A. The period of the function
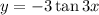 is
is
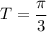
B. The period of the function
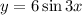 is
is

C. The period of the function
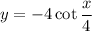 is
is
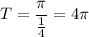
D. The period of the function
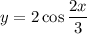 is
is
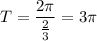
E. The period of the function
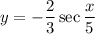 is
is