Question

If log2(13-8x)-log2(x^2+2)=2, what is the value of (13-8x/x^2+2)

Answer 1

4

Explanation:

There is a rule for logarithms that says:

`\log(a)-\log(b)=\log((a)/(b))`.

This is actually called quotient rule and it's name is based off the right hand side of the equation there.

So you have that you can write your right hand side as:

`\log_2((13-8x)/(x^2+2))`.

So your equation is:

`\log_2((13-8x)/(x^2+2))=2`

Now let's write this in the equivalent exponential notation:

`2^2=(13-8x)/(x^2+2)`

So the value of the given fraction is
`2^2=4`.

Note! In general, the equivalent exponential form of
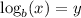`\log_b(x)=y` is
`b^y=x`.