Question

Prove that for every n E N, when we divide n2 by 7, the remainder is either 0, 1, 2, or 4. In other words, the remainder will never be 3, 5, or 6.

Answer 1

For every n E N, when we divide n² by 7, the remainder is either 0, 1, 2, or 4.

Explanation:

Given information: n∈N and
`(n^2)/(7)`.

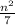To prove: For every n E N, when we divide n2 by 7, the remainder is either 0, 1, 2, or 4.

Proof:

Using basic remainder remainder theorem,

`remainder((n^2)/(7))=(remainder((n)/(7))* remainder((n)/(7)))(\text{mod }7)`

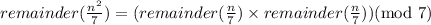
where, mod 7 is modulo 7. It means the remainder after dividing by 7.

If a natural number divide by 7 then the possible remainders are 0,1,2,3,4,5 and 6.

If remainder of n/7 is 0, then

`remainder((n^2)/(7))=(0* 0)(\text{mod }7)=0`

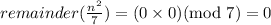
If remainder of n/7 is 1, then

`remainder((n^2)/(7))=(1* 1)(\text{mod }7)=1`

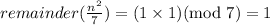
If remainder of n/7 is 2, then

`remainder((n^2)/(7))=(2* 2)(\text{mod }7)=4`

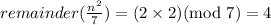
If remainder of n/7 is 3, then

`remainder((n^2)/(7))=(3* 3)(\text{mod }7)=9(\text{mod }7)=2`

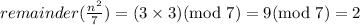
If remainder of n/7 is 4, then

`remainder((n^2)/(7))=(4* 4)(\text{mod }7)=16(\text{mod }7)=2`

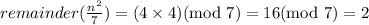
If remainder of n/7 is 5, then

`remainder((n^2)/(7))=(5* 5)(\text{mod }7)=25(\text{mod }7)=4`

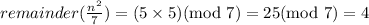
If remainder of n/7 is 6, then

`remainder((n^2)/(7))=(6* 6)(\text{mod }7)=36(\text{mod }7)=1`

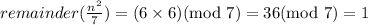
For every n E N, when we divide n2 by 7, the remainder is either 0, 1, 2, or 4.

Hence proved.