Question

Suppose f is the function f(x) = |x - 5| + 5 and f : Z -> Z

Is f one-to-one:

Is f onto:

Answer 1

No, function is not one-to-one

No, function is not onto

Explanation:

We are given that a function

f:
`Z\rightarrow Z`

`f(x)=\mid{x-5}\mid +5`

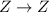
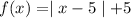
If function is one-to-one then different x have different image .

Domain =Z

Codomain=Z

When function is onto then range=Codomain

Substitute x=1

Then ,
`f(1)=\mid{1-5}\mid+5=4+5=9`

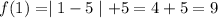
When substitute x=9

Then , we get
`f(9)=\mid {9-5}\mid +5=4+5=9`

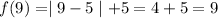
Image of 1 and 9 are same hence, function is not one-to-one.

Negative elements of Z and Zero has no preimage.Therefore, function is not onto.