Question

The absorbance of a 0.45 mol dm–3 solution of an aromatic amino acid, 3.0 cm thick is 0.22 at a wavelength of 295 nm:

(a) Calculate the molar absorption coefficient. [10 marks]

(b) What fraction of the incident light is transmitted by the solution if the absorbance was doubled to 0.44? [5 marks]

(c) What thickness of a 0.75 mol dm–3 solution would be required to transmit 65% of the incident radiation? [7 marks]

(d) Can you calculate the absorbance at 590 nm from the data provided? [3 marks]

Answer 1

Step-by-step explanation:

a) Using Beer-Lambert's law :

Formula used :

`A=\epsilon * C* l`

where,

A = absorbance of solution = 0.22

C = concentration of solution =
`0.45 mol/dm^3=0.45 mol/L=0.45 M`

`1 dm^3 = 1 L`

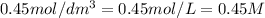
l = length of the cell = 3.0 cm

`\epsilon` = molar absorptivity of this solution = ?

Now put all the given values in the above formula, we get the molar absorptivity of this solution.

`0.22=\epsilon * (0.45 M)* (3.0 cm)`

`\epsilon=0.163 M^(-1)cm^(-1)`

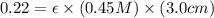
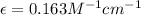
Therefore, the molar absorptivity of this solution is,
`1.93* 10^(4)M^(-1)cm^(-1)`

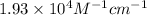
b)
`A=\log (I_o)/(I_t)`

`T=(I_t)/(I_o)`

`A=\log (1)/(T)`

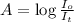
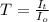
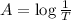
A = 2 × 0.22 =0.44

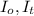`I_o,I_t` = Intensities of Incident light and transmitted light respectively

T = Transmittance

`0.44=\log (1)/(T)`

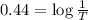
T = 0.3630

c)
`I_o=x`

`I_t=65\% of x=0.65 x`

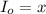
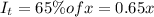
Thickness of cell = l' =?

`c = 0.75 mol/ dm^3=0.75 mol/L=0.75 M`

`A=\log (I_o)/(I_t)=\epsilon * C* l`

`\log (x)/(0.65x)=0.163 M^(-1)cm^(-1)* 0.45 M* l'`

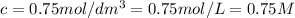
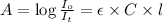
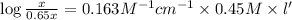
l' = 1.53 cm

d) No, we cannot calculate the absorbance at 590 nm from the given data. This is because absorbance at this wavelength can be observe experimentally.