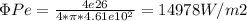Question

The surface temperature of a planet depends on both the distance of the planet from the Sun and on how the panet's atmosphere distributes energy. Mercury has a mass of 0.33 x 104 kg, a radius of 2440 km and it orbits the Sun in an elliptical orbit with a semi- major axis of 0.39 AU and eccentricity of 0.21. Assuming that the Sun radiates uniformly at a rate of 4 x 1026 W, cakculate the solar energy fhx (power incident m2 perpendicular to the Sun's rays), at Mercury's aphelion and perihelion.

Answer 1

Aphelion: 6404 W/m2

Perihelion: 14978 W/m2

Step-by-step explanation:

The solar energy flux depends on the solar power output divided by the surface of a sphere with a radius equal to the distance to the Sun.

`\Phi sol = (Psol)/(4 * \pi * d^2)`

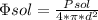
The distances we need are the aphelion and perihelion of Mercury.

Planetary orbits are ellipses. In an ellipse the eccentricity is related to linear eccentricity and the length of the semi major axis:

`e = (c)/(a)`

Where

e: eccentricity

c: linear eccentricity

a: semi major axis

The linear eccentricity is equal to the distance of the focus of the center of the ellipse.

`c = a * c =`

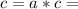
a = 0.39 AU = 5.83e10 m

`c = 5.83e10e * 0.21 = 1.22e10 m`

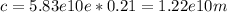
In planetary orbits the Sun is in one of the fucuses. With this we can calculate the prihelion and aphelion as:

Ap = a + c = 5.83e10 + 1.22e10 = 7.05e10 m

Pe = a - c = 5.83e10 - 1.22e10 = 4.61e10 m

And the solar energy fluxes will be:

`\Phi Ap = (4e26)/(4 * \pi * 7.05e10^2) = 6404 W/m2`

`\Phi Pe = (4e26)/(4 * \pi * 4.61e10^2) = 14978 W/m2`