Question

The half-life for the radioactive decay of iridium-192 is 74.2 days. Calculate the amount in grams of Ir-192 that will be left from a 13.65g sample after a) 199.2 days b) 350 days

Answer 1

Answer: There are

a) 2.12 g of Ir-192 after 199.2 days

b) 0.52 g of Ir-192 after 350 days

Step-by-step explanation:

Radioactive decay follows a first-order kinetics since the half life does not depend on the initial amount, then the equation which describes this process is:

`N(t)=N_(o)*e^{-(-0.693*t)/(t_(1/2) ) }`

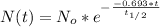
Where
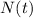`N(t)` is the amount given a certain t time, and
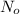`N_(o)` is the initial amount.
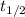`t_(1/2)` is the half life.

Then, the radioactive decay equation for this problem is:

`N(t)=13.65 g*e^{-(-0.693*t)/(74.2 days) }`

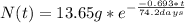
Note that the half life and the given time t must be on the same units, in this case days. Finally you calculate the amount for a) 199.2 days and b) 350 days:

`a) N(t)=13.65 g*e^{-(-0.693*199.2 days)/(74.2 days) }=2.12 g`

`b) N(t)=13.65 g*e^{-(-0.693*350 days)/(74.2 days) }=0.52 g`

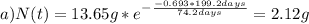
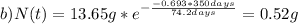
Hope it helps!