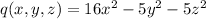Answer:
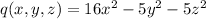
Explanation:
The given quadratic form is of the form
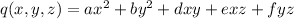 .
.
Where
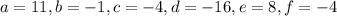 .Every quadratic form of this kind can be written as
.Every quadratic form of this kind can be written as
![q(x,y,z)={\bf x}^(T)A{\bf x}=ax^2+by^2+cz^2+dxy+exz+fyz=\left(\begin{array}{ccc}x&y&z\end{array}\right) \left(\begin{array}{ccc}a&(1)/(2) d&(1)/(2) e\\(1)/(2) d&b&(1)/(2) f\\(1)/(2) e&(1)/(2) f&c\end{array}\right) \left(\begin{array}{c}x&y&z\end{array}\right)]()
Observe that
 is a symmetric matrix. So
is a symmetric matrix. So
 is orthogonally diagonalizable, that is to say,
is orthogonally diagonalizable, that is to say,
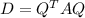 where
where
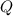 is an orthogonal matrix and
is an orthogonal matrix and
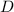 is a diagonal matrix.
is a diagonal matrix.
In our case we have:
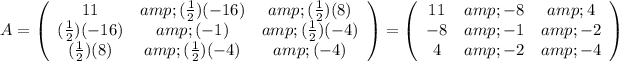
The eigenvalues of
 are
are
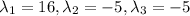 .
.
Every symmetric matriz is orthogonally diagonalizable. Applying the process of diagonalization by an orthogonal matrix we have that:

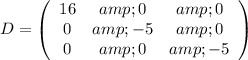
Now, we have to do the change of variables
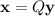 to obtain
to obtain

Which can be written as: