Question

Chris shoots an arrow up into the air. The height of the arrow is given by the function h(t) = - 16t2 + 32t + 26 where t is the time in seconds. What is the maximum height of the arrow?

Answer 1

The maximum height of the arrow is 42 (and the units given for the height)

Step-by-step explanation:

Everything is easier if you make a graph, you can give values to t and replace that values in the function, for example:

When t=0

`h(0)=-16(0^(2))+32(0)+26`

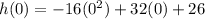
h(0)=26

If you give some values to t you can see how the trajectory of the arrow is (please look the graphic below)

Now, to find the maximum you have to find the derivative of the function that describes the height of the arrow:

`h(t)=-16t^(2)+32t+26`

`h'(t)=-32t+32`

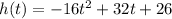
Then you have to take the derivative, and equals to zero to find t:

-32t+32=0

-32t=32

t=1

That is in the time of 1 second the arrow has its maximum height.

Now you have to replace this value in the original function, to find the height of the arrow:

`h(1)=-16(1^(2))+32(1)+26`

h(1)=-16+32+36

h(1)=42