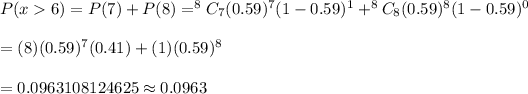Question

Fifty-nine percent of US adults have little confidence in their cars. You randomly select eight US adults. Find the probability that the number of US adults who have little confidence in their cars is (1) exactly three and then find the probability that it is (2) more than 6.

Answer 1

Answer: (1) 0.1332

(2) 0.0963

Explanation:

Given : The proportion of US adults have little confidence in their cars:p = 0.59

Sample size : n= 8

Using Binomial probability formula :-

`P(x)=^nC_xp^x(1-p)^(n-x)`

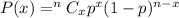
Then, the probability that the number of US adults who have little confidence in their cars is exactly three :-

`P(x=3)=^8C_3(0.59)^3(1-0.59)^(5)\\\\=(8!)/(3!(8-3)!)(0.59)^3(0.41)^(5)\\\\=0.133248811949\approx0.1332`

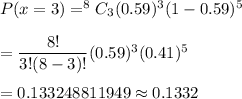
The probability that the number of US adults who have little confidence in their cars is more than 6:-

`P(x>6)=P(7)+P(8)=^8C_7(0.59)^7(1-0.59)^(1)+^8C_8(0.59)^8(1-0.59)^(0)\\\\=(8)(0.59)^7(0.41)+(1)(0.59)^8\\\\=0.0963108124625\approx0.0963`