Question

A ball is thrown downward from a cliff. Its position at time t seconds is given by the formula s(t) = 16t2 + 32t, where s is in feet. How many seconds (to the nearest tenth) will it take for the ball to fall 215 ft.? Round to the nearest tenth, if necessary.

Answer 1

It takes 2.8 seconds for the ball to fall 215 ft.

Explanation:

We are given a position function s(t) where s stands for the number of feet the ball has fallen, so we have to replace s with the given value of 215 ft and solve for the time t.

Setting up the equation.

The motion equation is given by

`s(t) =16t^2+32t`

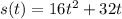
We can replace there s = 215 ft to get

`215=16t^2+32t`

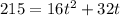
Solving for the time t.

From the previous equation we can move all terms in one side to get

`16t^2+32t-215=0`

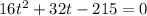
At this point we can solve for t using quadratic formula.

`t = \cfrac{-b\pm √(b^2-4ac)}{2a}`

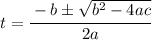
where a, b and c are the coefficients of the quadratic equation

`at^2+bt+c=0`

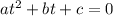
So we get

`a=16\\b=32\\c=-215`

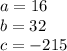
Replacing on the quadratic formula we get

`t = \cfrac{-32\pm √(32^2-4(16)(-215))}{2(16)}`

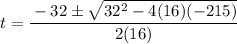
Using a calculator we get

`t=-4.8 , t = 2.8`

Physically speaking the only result that makes sense is to move forward in time that give us t = 2.8 seconds.

We can conclude that it takes 2.8 seconds for the ball to fall 215 ft.