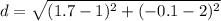Question

PROBLEM SOLVING You are participating in an orienteering competition. The diagram shows the position of a river that cuts through the woods. You are currently 2 miles east and 1 mile north of your starting point, the origin. What is the shortest distance you must travel to reach the river? Round your answer to the nearest tenth.

Answer 1

The shortest distance is 2.2 miles

Explanation:

we know that

The shortest distance you must travel to reach the river is the perpendicular distance to the river

step 1

Find the slope of the line perpendicular to the river

we have

`y=3x+2`

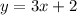
The slope of the river is m=3

Remember that if two lines are perpendicular, then their slopes are opposite reciprocal (the product of their slopes is -1)

therefore

The slope of the line perpendicular to the river is

`m=-1/3`

step 2

Find the equation of the line into point slope form

`y-y1=m(x-x1)`

we have

`m=-1/3`

`point(2,1)`

substitute

`y-1=-(1/3)(x-2)`

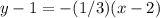
step 3

Find the intersection point of the river and the line perpendicular to the river

we have

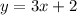`y=3x+2` ------> equation A

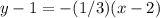`y-1=-(1/3)(x-2)` -----> equation B

Solve the system by graphing

The intersection point is (-0.1,1,7)

see the attached figure

step 3

Find the distance between the points (2,1) and (-0,1,1.7)

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

substitute

`d=\sqrt{(1.7-1)^(2)+(-0.1-2)^(2)}`

`d=\sqrt{(0.7)^(2)+(-2.1)^(2)}`

`d=2.2\ miles`