Question

If there are more than 20 observations in total or in the population, then the standard deviation of this data set (a sample from the population) is ___25, 45, 73, 16, 34, 98, 34, 45, 26, 2, 56, 97, 12, 445, 23, 63, 110, 12, 17, and 41

Answer 1

The standard deviation of this data set a sample from the population is equal to 94.9

Explanation:

We have 20 observations in total or in the population and we want to know the standard deviation of this data set.

The standard deviation formula to a sample from the population is:

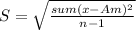`S=\sqrt{(sum(x-Am)^2)/(n-1)}` (1)

Where:

S: Standard deviation

sum: Summation

x: Sample values

Am: Arithmetic mean

n: Number of terms, in this case 20

Now, we need to know the arithmetic mean of the sample values

`Am=(25+45+73+16+34+98+34+45+26+2+56+97+12+445+23+63+110+12+17+41)/(20)`

`Am=(1274)/(20)\\ Am=63.7`

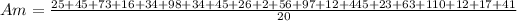
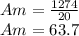
To know the standard deviation we need to have the summation of each term minus the arithmetic mean squared.

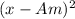`(x-Am)^2` of each term:

`(25-63.7)^2=1497.69\\(45-63.7)^2=349.69\\(73-63.7)^2=86.49\\(16-63.7)^2=2275.29\\(34-63.7)^2=882.09\\(98-63.7)^2=1176.49\\(34-63.7)^2=882.09\\(45-63.7)^2=349.69\\(26-63.7)^2=1421.29\\(2-63.7)^2=3806.89\\(56-63.7)^2=59.29\\(97-63.7)^2=1108.89\\(12-63.7)^2=2672.89\\(445-63.7)^2=145390\\(23-63.7)^2=1656.49\\(63-63.7)^2=0.49\\(110-63.7)^2=2143.69\\(12-63.7)^2=2672.89\\(17-63.7)^2=2180.89\\(41-63.7)^2=515.29`

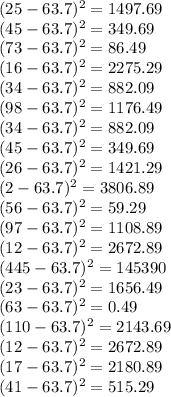
The summation of each term minus the arithmetic mean squared is: 171128.2

Now, we can find the standard deviation with the equation (1)

`S=\sqrt{(sum(x-Am)^2)/(n-1)}`

`S=\sqrt{(171128.2)/(20-1)}\\S=\sqrt{(171128.2)/(19)}\\S=√(9006.75) \\S=94.9`

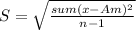
The standard deviation is equal to 94.9