Answer:
The point of division is (5 , 8)
Explanation:
* Lets explain how to solve the problem
- If point (x , y) divides the line whose endpoints are

and
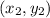 at ratio
at ratio
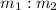 , then
, then
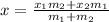 and
and
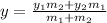
* Lets solve the problem
- The directed line segment with endpoints A (3 , 2) and B (6 , 11)
- There is a point divides AB two-thirds from A to B
∵ The coordinates of the endpoints of the directed line segments
are A = (3 , 2) and B = (6 , 11)
∴
 is (3 , 2)
is (3 , 2)
∴
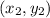 is (6 , 11)
is (6 , 11)
∵ Point (x , y) divides AB two-thirds from A to B
- That means the distance from A to the point (x , y) is 2/3 from
the distance of the line AB, and the distance from the point (x , y)
to point B is 1/3 from the distance of the line AB
∴
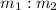 = 2 : 1
= 2 : 1
∵
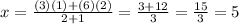
∴ The x-coordinate of the point of division is 5
∵
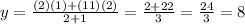
∴ The y-coordinate of the point of division is 8
∴ The point of division is (5 , 8)