Question

A parabola intersects the x-axis at x = 3 and x = 9.

What is the x-coordinate of the parabola's vertex?

Answer 1

6

Explanation:

This function corresponds to 'even' function, then

in order to calculate the 'x' of the vertex: (3+9)/2=6.

Answer 2

The x-coordinate of the parabola's vertex is 6.

Explanation:

A parabola in the following format:

`y = ax^(2) + bx + c`

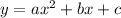
With

`\Delta = b^(2) - 4ac`

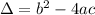
Has the following vertex:

`V = (x_(v), y_(v))`

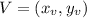
In which

`x_(v) = -(b)/(2a)`

`y_(v) = -(\Delta)/(4a)`

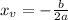
In this problem, we have that:

A parabola intersects the x-axis at x = 3 and x = 9. This means that the roots are x = 3 and x = 9, and that our parabola is defined by the following equation:

`y = (x - 3)(x - 9) = x^(2) - 12x + 27`

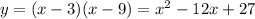
So

`x = 1, b = -12, c = 27`

`x_(v) = -(b)/(2a) = -(-12)/(2) = 6`

The x-coordinate of the parabola's vertex is 6.