Question

The Parliament Building tower clock in London, has hour and minute hands with lengths of 2.70 m and 4.50 m and masses of 60.0 kg and 100 kg, respectively. Calculate the total angular momentum of these hands about the center point. Treat the hands as long, thin uniform rods.

Answer 1

The total angular momentum of these hands is 1.20 kg m²/s.

Step-by-step explanation:

Given that,

Length of hour hand = 2.70 m

Length of minute hand = 4.50 m

Mass of hour hand = 60.0 kg

Mass of minute hand = 100 kg

We need to calculate the total angular momentum

Using formula of angular momentum

`L=I_(k)\omega_(k)+I_(m)\omega_(m)`

`L=((ml_(h)^2)/(3))*(2\pi)/(T)+(ml_(m)^2)/(3)*(2\pi)/(T)`

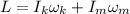
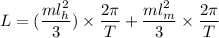
Where,
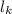`l_(k)` = length of hour hand

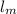`l_(m)`=length of minute hand

Put the value into the formula

`L=(60.0*(2.70)^2)/(3)*(2\pi)/(12*3600)+(100*(4.50)^2)/(3)*(2\pi)/(3600)`

`L=1.199 = 1.20\ kg m^2/s`

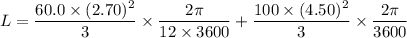
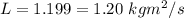
Hence, The total angular momentum of these hands is 1.20 kg m²/s.

Answer 2

Step-by-step explanation:
`1.1993 kg-m^2/s`

Given

length of hour hand is 2.7m

length if minute hand is 4.5m

And Moment of inertia of a rod about its one of a end
`I=(ml^2)/(3)`

`\omega`for hour hand is

`\omega =(2\pi )/(12\cdot 3600) rad/s`

Angular speed for minute hand
`=frac{2\pi }{3600}`

Angular moment(L) is given
`I\omega`

`L_(minute)=(100* 4.5^2)/(3)* frac{2\pi }{3600}`

`L_(minute)=1.178`

For hour hand

`L_(hour)=(ml^2)/(3)\omega`

`L_(hour)=(60* 2.7^2)/(3)* (2\pi )/(12\cdot 3600)`

`L_(hour)=0.0212 kg-m^2/s`

`L_(total)=1.1993 kg-m^2/s`