Question

Terrance claims that for the input coordinates (x, y), a rotation of 180° clockwise about the origin, followed by a reflection over the line y = x, results in output coordinates of (x, y), since the two transformations cancel themselves out.

Decide if Terrance is correct. If he is correct, enter (x, y) below. If he is not correct, enter the correct output coordinates for the input coordinates (x, y) after a rotation of 180° clockwise about the origin and a reflection over the line y = x.

Answer 1

Terrance is incorect.

Correct output coordinates (-y,-x)

Explanation:

Let
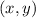`(x,y)` be the input coordinates.

First translation is a rotation of 180° clockwise about the origin. This translation has a rule

`(x,y)\rightarrow (-x,-y)`

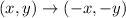
Second translation is a reflection over the line y = x. The general rule for the reflection across the line y=x has the rule

`(a,b)\rightarrow (b,a)`

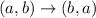
When a sequence of two translations are applied to the initial input coordinates, then

`(x,y)\rightarrow (-x,-y)\rightarrow (-y,-x)`

As you can see Terrance made a mistake and these two transformations do not cancel themselves out.