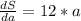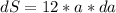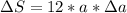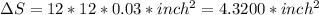Question

The measurement ol the edge of a cube is found to be 12 inches, with a possible error of 0.03 inch. Use differentials to approximate the maximum possible propagated error in computing the volume of the cube and the surface area of the cube. (Round your answers to four decimal places.)

Answer 1

`\Delta V= 12.9600*inch^(3) \\\Delta S=4.3200*inch^(2)`

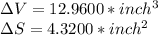
Explanation:

Hello!

In order to solve this problem we'll start by writing down the data below:

`a=(12\pm0.03)* inch`

`da\approx \Delta a=0.03*inch`

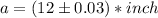
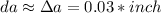
Now we are going to define two functions, the volume and the surface area of the cube in function of the measured edge a:

volume:
`V(a)=a^(3)`

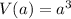
surface area:
`S(a)=6*a^(2)`

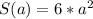
Ok so, for the maximum possible propagated error in computing the volume of the cube. We derivate V(a) and obtain:

`(dV)/(da)= 3*a^(2)`

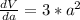
solve for dV and compute:

`dV=3*a^(2)*da`

`\Delta V= 3*a^(2)*\Delta a`

`\Delta V=3*12^(2)*0.03* inch^(3)=12.9600*inch^(3)`

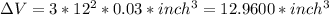
There it is for the volume...

Now we'll proceed to do exactly the same but with the function S(a):

`(dS)/(da) =12*a`

`dS=12*a*da`

`\Delta S=12*a*\Delta a`

`\Delta S= 12*12*0.03*inch^(2)=4.3200 *inch^(2)`