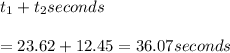Question

A speeder traveling at a constant speed of 111 km/h races past a billboard. A patrol car pursues from rest with constant acceleration of (7 km/h)/s until it reaches its maximum speed of 165 km/h, which it maintains until it catches up with the speeder. How long does it take the patrol car to catch the speeder if it starts moving just as the speeder passes

Answer 1

Thus the speeder is caught after
`36.07seconds`

Step-by-step explanation:

When the patrol car catches the speeder both of them would have traveled the same distance and traveled for same time. Let the distance covered be 'd' and the time required be time 't'.

The given values are converted to SI units as under

`u_(s)=111km/h=(111* 10^(3))/(3600)=30.83m/s\\\\a_(p)=7kmh^(-1)/s=(7* 10^(3))/(3600)m/s^(2)=1.94m/s^(2)\\\\v_(f)=165km/h=(165* 10^(3))/(3600)=45.83m/s`

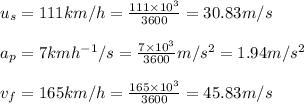
The time in which patrol car reaches speed of 165 km/h can be calculated from the first equation of kinematics as

`v=u+at`

`45.83=0+1.94t\\\\\therefore t=(45.83)/(1.94)=23.62s`

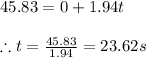
The distance covered by both the cars in this time

`d_(speeder)=30.83* 23.62=728.20m\\\\d_(patrol)=(1)/(2)* 1.94* 23.62^(2)=541.16m`

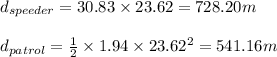
Now the remaining distance will be covered in same time

Thus we have

`d-728.20=30.83* t_(2)........(i)\\\\d-541.16=45.83* t_(2).........(ii)\\\\`

Thus solving equation i and ii we get

`45.83t_(2)+541.16-728.20=30.83t_(2)\\\\45.83t_(2)-30.83t_(2)=728.20-541.16\\\\\therefore t_(2)=(187.04)/(15)=12.45s`

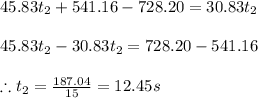
Thus the speeder is caught after
`t_(1)+t_(2)seconds\\\\=23.62+12.45=36.07seconds`