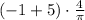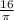Answer:
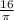
Explanation:
The average rate of a function
 on interval
on interval
 to
to
 is:
is:
 .
.
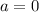 and
and
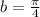 here for this problem where
here for this problem where
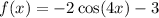 .
.
So we will need to evaluate
 for
for
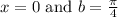 .
.
To find
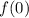 we will replace
we will replace
 in
in
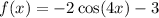 with
with
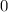 :
:
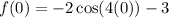
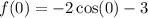
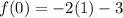
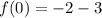
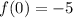
To find
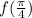 we will replace
we will replace
 in
in
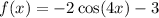 with
with
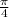 :
:

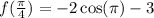
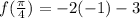

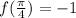
So now we need to compute the change in
 over the change in
over the change in
 :
:
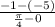
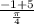
Dividing by
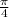 is the same as multiplying by
is the same as multiplying by
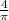 :
: