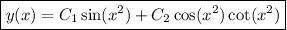Question

Consider the equation

xy'' - y' + 4x^(3)y = 0

Show that y1(x) = sin(x^2) is a solution

Find the second solution by letting y = u(x)y1 (x) and solve for u(x)

Write the complete general solution

Answer 1

`y_1=\sin(x^2)\implies{y_1}'=2x\cos(x^2)\implies{y_1}''=2\cos(x^2)-4x^2\sin(x^2)`

Substituting
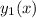`y_1(x)` and its derivatives into the ODE gives

`x\left(2\cos(x^2)-4x^2\sin(x^2)\right)-2x\cos(x^2)+4x^3\sin(x^2)=0`

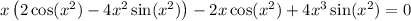
as required.

Assume a second solution of the form
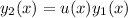`y_2(x)=u(x)y_1(x)`. Then

`y_2=uy_1\implies{y_2}'=u'y_1+u{y_1}'\implies{y_2}''=u''y_1+2u'{y_1}'+u{y_1}''`

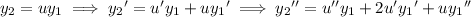
Substitute these into the ODE:

`x(u''y_1+2u'{y_1}'+u{y_1}'')-(u'y_1+u{y_1}')+4x^3uy_1=0`

`x\sin(x^2)u''+\left(4x^2\cos(x^2)-\sin(x^2)\right)u'=0`

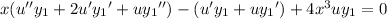
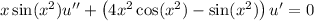
This ODE is separable as

`\implies(\mathrm du'')/(\mathrm du)=(\sin(x^2)-4x^2\cos(x^2))/(x\sin(x^2))\,\mathrm dx`

Integrating both sides gives

`\ln|u'|=\displaystyle\int\left(\frac1x-4x\cot(x^2)\right)\,\mathrm dx`

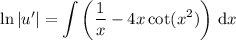
For the remaining integral, we have

`\displaystyle\int\frac{\mathrm dx}x=\ln|x|+C`

`\displaystyle\int4x\cot(x^2)\,\mathrm dx=2\int\cot(x^2)(2x\,\mathrm dx)=2\ln|\sin(x^2)|+C`

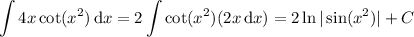
So we have

`\ln|u'|=\ln|x|-2\ln|\sin(x^2)|+C`

`\implies u'=Cx\csc^2(x^2)`

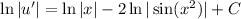
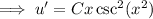
Integrate both sides to solve for
`u(x)`:

`\displaystyle\int u'\,\mathrm dx=C\int x\csc^2(x^2)\,\mathrm dx`

`\implies u=\displaystyle\frac C2\int\csc^2(x^2)(2x\,\mathrm dx)`

`\implies u=C_1\cot^2(x^2)+C_2`

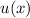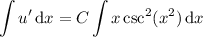
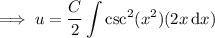
Then our second solution turns out to be

`y_2=uy_1=C_1\cot^2(x^2)\sin(x^2)+C_2\sin(x^2)`

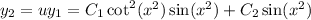
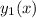`y_1(x)` already captures the second term here, so the second fundamental solution is

`\boxed{y_2(x)=\cos(x^2)\cot(x^2)}`

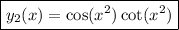
and the general solution is

`\boxed{y(x)=C_1\sin(x^2)+C_2\cos(x^2)\cot(x^2)}`