Question

Correct answers only please!

Credit Cards have 16 digit numbers, of which the first 15 digits identify the credit card and the sixteenth digit is the check digit (the last digit is fixed). U-Kan-Trust-Us Credit Card numbers begin with 61, 62, or 63. What is the maximum number of credit cards that UKTU can issue?


A. 3 ( 10^12)


B. 3 (10^13)


C. 3 (10^14)


D. 3 (10^15)

Answer 1

The correct option is B.

Explanation:

Total possible digits are 0,1,2,3,4,5,6,7,8,9.

Total number of digits in a credit card = 16

It is given that that the last digit of credit card is fixed.

Total number of possible ways for 16th digit = 1

U-Kan-Trust-Us Credit Card numbers begin with 61, 62, or 63.

Total number of possible ways for first two digits = 3

Remaining places = 16 - 1 - 2 = 13

In these 13 remaining places any of 10 digits can be occur.

Total number of possible ways for remaining 13 digits =
`10^(13)`

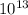
The maximum number of credit cards that UKTU can issue is

`Total =3* (10^(13))* 1`

`Total =3(10^(13))`

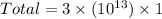
Therefore the correct option is B.

Answer 2

B. 3×10^13

Explanation:

The first two digits are fixed at one of three pairs of values; the last digit is "fixed" as the check digit, leaving 16 - 3 = 13 free digits. These can take on any of 10^13 values.

The total number of possible card numbers is 3×10^13.