Question

Charged particles q1=− 4.80 nC and q2=+ 4.80 nC are separated by distance 3.00 mm , forming an electric dipole. The charges are in a uniform electric field whose direction makes an angle 36.4° with the line connecting the charges. What is the magnitude of this field if the torque exerted on the dipole has magnitude 8.00×10^−9 N⋅m ?

Answer 1

Electric field, E = 936.19 N/C

Step-by-step explanation:

It is given that,

Charge 1,
`q_1=-4.8\ nC=-4.8* 10^(-9)\ C`

Charge 2,
`q_2=+4.8\ nC=+4.8* 10^(-9)\ C`

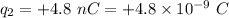
Distance between them, d = 3 mm = 0.003 m

Torque,
`\tau=8* 10^(-9)\ N-m`

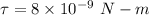
Angle between electric field and line connecting the charge,
`\theta=36.4^(\circ)`

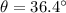
We need to find the torque exerted on the dipole. The torque experienced by the dipole in the electric field is given by :

`\tau=pE\ sin\theta`

p is the dipole moment,
`p=qd`

`\tau=qdE\ sin\theta`

`E=(\tau)/(qd\ sin\theta)`

`E=(8* 10^(-9))/(4.8* 10^(-9)* 0.003\ sin(36.4))`

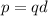
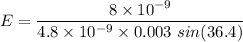
E = 936.19 N/C

So, the magnitude of electric field on the dipole is 936.19 N/C. Hence, this is the required solution.