15. B: If
 is non-zero, then
is non-zero, then
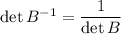 . We have
. We have

so
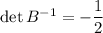
16. C: In general,
 for two matrices
for two matrices
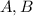 , but equality holds if
, but equality holds if
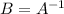 . D is incorrect because
. D is incorrect because
 .
.
17. C: This follows from a property of the determinant:
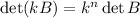
where
 is the size of the (square) matrix
is the size of the (square) matrix
 (and "size" refers to the number of rows or columns, both of which are the same).
(and "size" refers to the number of rows or columns, both of which are the same).
18. A: A matrix has no inverse if its determinant is 0. The determinant of (A) is 0 because it contains a row made up entirely of 0s.
19. B: The matrix product
 only exists if the number of columns of
only exists if the number of columns of
 is equal to the number of rows of
is equal to the number of rows of
 . In (a), the first matrix has 1 column and the other has 2 rows, so multiplication is invalid. In (c), the product on the left side would produce
. In (a), the first matrix has 1 column and the other has 2 rows, so multiplication is invalid. In (c), the product on the left side would produce
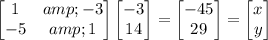
so that
 and
and
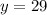 , but these values don't work with the given equations because -45 - 3(29) = -132, not -3. In (d), the product on the left side is
, but these values don't work with the given equations because -45 - 3(29) = -132, not -3. In (d), the product on the left side is
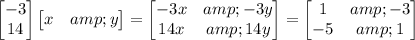
but then this would mean both
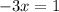 and
and
 , which are not consistent and have no solution.
, which are not consistent and have no solution.