Step-by-step explanation:
When two immiscible liquids are separated out at their boundary when they are present in two sections then there occurs an increase in their surface energy and it is known as work of adhesion.
It is given that contact angle for water on paraffin is
 and temperature is
and temperature is
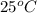 .
.
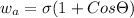
where,
 = contact angle
= contact angle
 = surface tension for water
= surface tension for water
Here, the two immiscible liquids are water and paraffin. Also, it is known that at
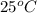 ,
,
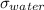 is 72 dynes/cm.
is 72 dynes/cm.
Hence, work of adhesion will be calculated as follows.
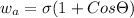
=
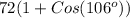
= -19.84 dynes/cm
Hence, the work of adhesion is -19.84 dynes/cm.
When we separate out a column of pure liquid into two halves then there occurs an increase in free energy. This is known as cohesion.
Expression for work of cohesion is given as follows.
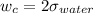
=

= 144 dynes/cm
Hence, the work of cohesion is 144 dynes/cm.
The difference between work of adhesion and work of cohesion is known as spreading coefficient.
S =

= -19.84 dynes/cm - 144 dynes/cm
= - 163.84 dynes/cm
Hence, the spreading coefficient is - 163.84 dynes/cm.