Question

Find the probability of being dealt a full house. (Round your answer to six decimal places.)?

Answer 1

I'm assuming a 5-card hand being dealt from a standard 52-card deck, and that there are no wild cards.

A full house is made up of a 3-of-a-kind and a 2-pair, both of different values since a 5-of-a-kind is impossible without wild cards.

Suppose we fix both card values, say aces and 2s. We get a full house if we are dealt 2 aces and 3 2s, or 3 aces and 2 2s.

The number of ways of drawing 2 aces and 3 2s is

`\dbinom42\dbinom43=24`

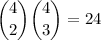
and the number of ways of drawing 3 aces and 2 2s is the same,

`\dbinom43\dbinom42=24`

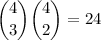
so that for any two card values involved, there are 2*24 = 48 ways of getting a full house.

Now, count how many ways there are of doing this for any two choices of card value. Of 13 possible values, we are picking 2, so the total number of ways of getting a full house for any 2 values is

`2\dbinom{13}2\dbinom42\dbinom43=3744`

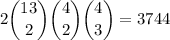
The total number of hands that can be drawn is

`\dbinom{52}5=2,598,960`

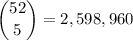
Then the probability of getting a full house is

`\frac{2\binom{13}2\binom42\binom43}{\binom{52}5}=\frac6{4165}\approx\boxed{0.001441}`