Answer: 0.5
Explanation:
Binomial distribution
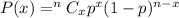 , where P(x) is the probability of getting success inn x trials , n is the number of trails and p is the probability of getting success in each trial.
, where P(x) is the probability of getting success inn x trials , n is the number of trails and p is the probability of getting success in each trial.
Given : Sarah times her morning commute such that there is an equal likelihood that she will arrive early or late to work on any given day.
Then , the probability that Sarah is late on particular day =
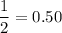
Then , the probability that Sarah will arrive late to work no more than twice during a five day workweek :-
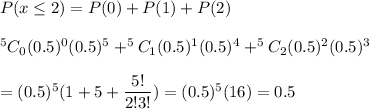
Hence, the required probability : 0.5