Answer:
The domain:
Interval:
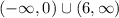
Inequality: x<0 or x>6
Words: x is less than 0 or greater than 6.
The range:
Interval:
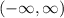
Inequality:
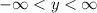
Words: All real numbers.
Explanation:
For the natural log (Ln) to exist, the inside must be positive.
So the domain can be found by solving the following:

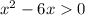
Let's factor:
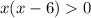
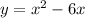 is a faced up parabola with x-intercepts x=0 and x=6. This means it is positive when x<0 or when x>6. Those are the parts with the curve of the parabola is above the x-axis.
is a faced up parabola with x-intercepts x=0 and x=6. This means it is positive when x<0 or when x>6. Those are the parts with the curve of the parabola is above the x-axis.
So the domain is x<0 or x>6.
Interval notation if you prefer would be:
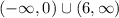 .
.
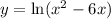 as equivalent exponential form
as equivalent exponential form
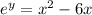 .
.
So let's look at the parabola one more time....
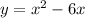 has it's minimum occur halfway between the x-intercepts we found earlier. Parabolas are symmetric about their axis of symmetry which the vertex lays on. So the halfway point of x=0 and x=6 is x=3. The vertex occurs at x=3.
has it's minimum occur halfway between the x-intercepts we found earlier. Parabolas are symmetric about their axis of symmetry which the vertex lays on. So the halfway point of x=0 and x=6 is x=3. The vertex occurs at x=3.
To find the corresponding y-coordinate we can replace x with 3:
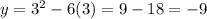 .
.
The lowest point is -9 since the parabola is opened up.
So we know that
 .
.
We also know every exponential function is greater than 0 so the intersections of what I just mentioned about our
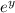 and all exponential functions is just >0.
and all exponential functions is just >0.
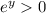 for all
for all

So the range is all real numbers.
As an inequality:
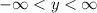
As an interval:
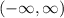 .
.