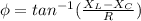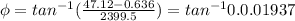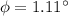Given:
Inductance, L = 150 mH
Capacitance, C = 5.00 mF
 = 240 V
= 240 V
frequency, f = 50Hz
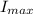 = 100 mA
= 100 mA
Solution:
To calculate the parameters of the given circuit series RLC circuit:
angular frequency,
 =
=
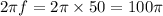
a). Inductive reactance,
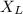 is given by:
is given by:
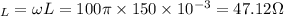
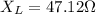
b). The capacitive reactance,
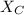 is given by:
is given by:

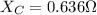
c). Impedance, Z =
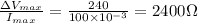
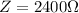
d). Resistance, R is given by:
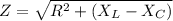
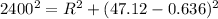
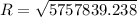

e). Phase angle between current and the generator voltage is given by: