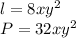A square has an area of 64x^2y^4. What is its side lenght and perimeter

Question

asked Sep 12, 2020 131k views

2 Answers

Nixmd · Answer 1 · 2020-09-13T01:55:45+0000

Answer:

Side length = 8xy^2

Perimeter = 32xy^2.

Explanation:

As it's a square the side length is the square root of the area

= √ (64x^2y^4)

= 8xy^2.

The perimeter is 4 times this.

Mahir · Answer 2 · 2020-09-17T04:52:37+0000

For this case we have that by definition, the area of a square is given by:
A = l ^ 2

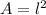
Where:

l: It's the side of the square

We have as data that:

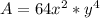
A = 64x ^ 2 * y ^ 4

So:

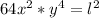
64x ^ 2 * y ^ 4 = l ^ 2

We cleared l, applying root to both sides:

$l = \pm \sqrt {64x ^ 2 * y ^ 4}$

We choose the positive value of the root:

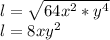
$l = \sqrt {64x ^ 2 * y ^ 4}\\l = 8xy ^ 2$

So, the side of the square is:
8xy ^ 2

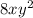
The perimeter is given by:

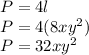
$P = 4l\\P = 4 (8xy ^ 2)\\P = 32xy ^ 2$

Answer:

$l = 8xy ^ 2\\P = 32xy ^ 2$