Question

Identify the parameter p in the following binomial distribution scenario. The probability of buying a movie ticket with a popcorn coupon is 0.711 and without a popcorn coupon is 0.289. If you buy 21 movie tickets, we want to know the probability that more than 14 of the tickets have popcorn coupons. (Consider tickets with popcorn coupons as successes in the binomial distribution.)

Answer 1

Answer: p=0.711

Explanation:

The binomial distribution probability formula :-

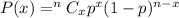`P(x)=^nC_xp^x(1-p)^(n-x)` , where P(X) is the probability of success in x trials , p is the probability of success in each trial and n is the total number of trials .

Given : The probability of buying a movie ticket with a popcorn coupon is 0.711 and without a popcorn coupon is 0.289.

If you buy 21 movie tickets, we want to know the probability that more than 14 of the tickets have popcorn coupons.

Then, the event of success is tickets have popcorn coupons.

Hence, the parameter p for the given binomial distribution scenario : p=0.711