Question

A roller of radius 14.25 cm turns at 10 revolutions per second. What is the linear velocity of the roller in meters per second?

Answer 1

A point on the edge of the roller travels the circumference of the roller in 1 revolution, so that its linear velocity is

(10 rev/s) * (2*(14.25 cm)*pi cm/rev) = 285 pi cm/s

or about 895.4 cm/s.

Answer 2

Linear velocity, v = 8.95 m/s

Explanation:

It is given that,

Radius of the roller, r = 14.25 cm = 0.1425 m

Angular velocity,
`\omega=10\ rev/s=62.83\ rad/s`

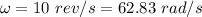
We need to find the linear velocity of the roller. Th linear velocity of the roller is given by :

`v=r* \omega`

`v=0.1425* 62.83`

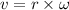
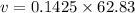
v = 8.95 m/s

So, the linear velocity of the roller is 8.95 m/s. Hence, this is the required solution.