Question

A 160-inch strip of metal 20 inches wide is to be made into a small open trough by bending up two sides on the long side, at right angles to the base. The sides will be the same height, x. If the trough is to have a maximum volume, how many inches should be turned up on each side?

Answer 1

The question above is right!

Explanation:

I double checked and took the test its all correct!

Answer 2

The value of double derivative at x=4.834 is negative, therefore the trough have a maximum volume at x=4.834 inches.

Explanation:

The dimensions of given metal strip are

Length = 160 inch

Width = 20 inch

Let the side bend x inch from each sides to make a open box.

Dimensions of the box are

Length = 160-2x inch

Breadth = 20-2x inch

Height = x inch

The volume of a cuboid is

`V=length* breadth * height`

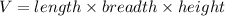
Volume of box is

`V(x)=(160-2x)* (20-2x)* x`

`V(x)=(160-2x)(20-2x)x`

`V(x)=4 x^3 - 360 x^2 + 3200 x`

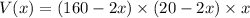
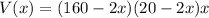
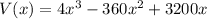
Differentiate with respect to x.

`V'(x)=12x^2 - 720 x + 3200`

Equate V'(x)=0, to find the critical points.

`0=12x^2 - 720 x + 3200`

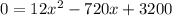
Using quadratic formula,

`x=30\pm 10\sqrt{(\left(19\right))/(3)}`

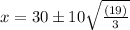
The critical values are

`x_1=30+10\sqrt{(\left(19\right))/(3)}\approx 55.166`

`x_2=30-10\sqrt{(\left(19\right))/(3)}\approx 4.834`

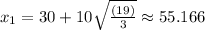
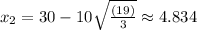
Differentiate V'(x) with respect to x.

`V'(x)=24x - 720`

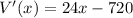
The value of double derivative at critical points are

`V'(55.166)=24(55.166) - 720=603.984`

`V'(4.834)=24(4.834) - 720=-603.984`

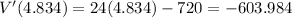
Since the value of double derivative at x=4.834 is negative, therefore the trough have a maximum volume at x=4.834 inches.