Question

A hair dryer is basically a duct of constant diameter in which a few layers of electric resistors are placed. A small fan pulls the air in and forces it through the resistors where it is heated. If the density of air is 1.20 kg/m3 at the inlet and 1.035 kg/m3 at the exit, determine the percent increase in the velocity

Answer 1

The percent increase in the velocity is 15.9%.

Step-by-step explanation:

Given that,

Density of air
`\rho_(in)= 1.20\ kg/m^3`

Density of air
`\rho_(ex)=1.035\ kg/m^3`

We need to calculate the percent increase in the velocity

Using continuity equation

`\rho_(in)Av=\rho_(ex)Av'`

`(\rho_(in))/(\rho_(ex))=(v')/(v)`

Put the value into the formula

`(v')/(v)=(1.20)/(1.035)`

`(v')/(v)=1.159`

`v'=1.159v`

For percentage,

`v'=(1.159v-v)/(v)*100`

`v'=15.9\%`

Hence, The percent increase in the velocity is 15.9%.

Answer 2

Given:

density of air at inlet,
`\rho_(a) = 1.20 kg/m_(3)`

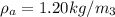
density of air at inlet,
`\rho_(b) = 1.05 kg/m_(3)`

Solution:

Now,

`\dot{m} = \dot{m_(a)} = \dot{m_(b)}`

`\rho_(a) A v_(a) = \rho _(b) Av_(b)` (1)

where

A = Area of cross section

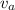`v_(a)` = velocity of air at inlet

`v_(b)` = velocity of air at outlet

Now, using eqn (1), we get:

`(v_(b))/(v_(a)) = (\rho_(a))/(\rho_(b))`

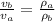
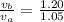`(v_(b))/(v_(a)) = (1.20)/(1.05)` = 1.14

% increase in velocity =
`1.14* 100` =114%

which is 14% more

Therefore % increase in velocity is 14%